Life Sciences - Research Groups
Quandt Research Group: Mathematical Immuno-Epidemiology

The understanding of complex biological systems requires the reconstruction of multiscale processes, occurring on multiple spatial and temporal scales.
Our group works at the development of analytical and computational techniques for the description of processes arising in immunology and infectious diseases. In particular, we work on
(i) in-host phenomena at intracellular level (e.g. signaling pathways),
or at cellular level (e.g. interactions of immune cells with infected cells or tumor cells)
(ii) between-hosts dynamics (e.g. pathogen transmission and social dynamics)
and on the coupling of these two scales. This allows, for example, to capture the effects of individual immunity on epidemiological outbreaks in a population, or to study molecular mechanisms and events that influence the dynamic at cellular level (e.g. cell proliferation, death, functionality).
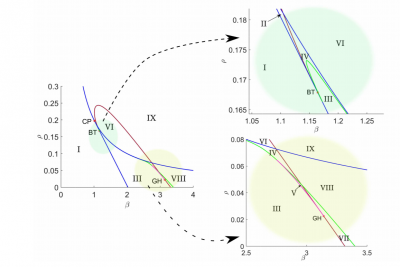
Combining elements of nonlinear and infinite-dimensional dynamics with numerical simulations and optimization, we aim at both qualitative and quantitative understanding of biological phenomena.
Research
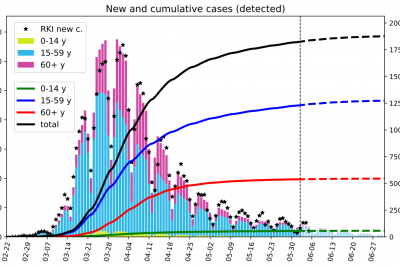
COVID-19
Models and Simulations on the COVID-19 pandemic
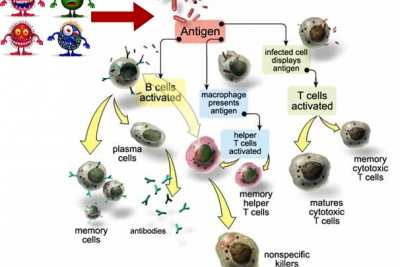
Mathematical Immunology
Inflammation and Immune Response