Research Group Franziska Matthäus – Topics
Agent-based modelling
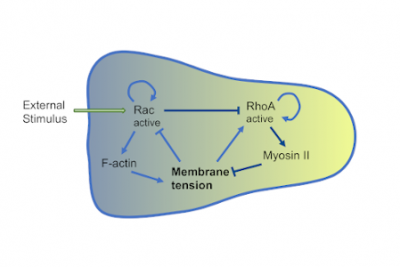
Mathematical models are useful tools to understand the coordinated behaviour of multicellular systems. We use agent-based models and simulations in order to investigate how mechanical interactions coupled with chemical cues give rise to orchestrated multicellular behaviour. To this end, ordinary differential equations, governing the mechanical properties of single cells are coupled to partial differential equations describing the chemical environment of the cells. In addition intercellular biochemical pathways can be taken into account. We use (hybrid) agent based models to understand processes during embryo development in several systems (red flower beetle, skin patterning in mouse, stem cell fate decision), the dynamics of experimental model systems such as organoids or spheroids, and collective cell migration in cancer cell lines. On the technical side we pursue efficient simulation strategies, i.e. by GPU implementation of the models.

Density-based modelling
Currently we are developing a model for skin patterning, given as a system of coupled partial differential equations, describing the dynamics of the local cell density and the local concentration of interacting diffusible chemical components. The model couples two distinct patterning processes, a reaction-diffusion (Turing-type) mechanism, and chemotaxis. Although both systems have been studied extensively in the past, both mathematically and experimentally, only recently it became evident, that they interact in the process of hair follicle formation. Therefore, we explore using numerical and mathematical analysis, how the interaction of these processes affects the conditions for the appearance of patterns, as well shape and regularity of the resulting patterns.

Image Processing
In order to gain quantitative relations and parameters on the systems behavior we use various image processing tools, such as segmentation, morphological analysis, single-cell tracking or particle image velocimetry (PIV). PIV is a correlation-based technique to obtain spatio-temporal velocity distributions for collectively moving or deforming tissues. In contrast to single-cell tracking, PIV does not rely on cell segmentation and can therefore be applied also to time-lapse images of unstained tissue material. Recently, we have developed a Julia package for 3D PIV, enabling the analysis of dynamic 3D microscopy data. Further, we use segmentation and polygonal cell shape approximation as a pre-step in the inference of mechanical properties of confluent epithelial layers.
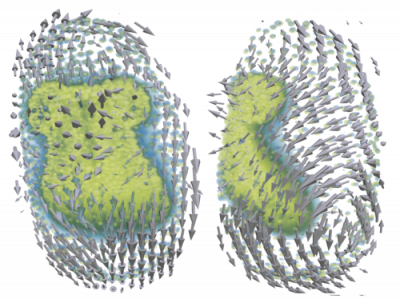
Inference of mechanical properties
Force Inference (FI) is a computational approach to estimate tissue stress from static images using a biomechanical model and a mathematical inverse method. To gain further insights into the multi-scale effects of force propagation from cells to tissues and the shaping properties on whole organisms, it is of great interest to study spatial and temporal dynamics of forces. As a non-invasive observation technique, FI requires no mechanical probing of the tissue and yields results for the whole system at once. We work inside a Bayesian framework to handle the topology-bound indefiniteness in a system of linear force-balance equations. We use FI to investigate force dynamics in time-lapse data like wound healing assays and 3D data from embryogenesis of Tribolium castaneum.