Research of Ivan Kisel
Overview
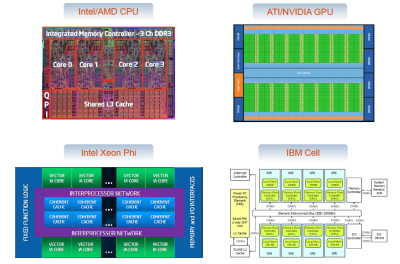
The track and particle reconstruction is a task, which needs a lot of computational power. At the same time all modern high energy physics experiments operate with huge data rates and require fast reconstruction procedures. In order to operate effectively in such difficult conditions the full utilization of the computer power is required. Parallel programing is considered now as the only way to utilize the full power of CPU and GPU, since all modern CPUs and GPUs have more than one core. They are also equipped with SIMD units. Therefore the developed algorithms are implemented using:
- headers overloading SIMD instructions and a Vc library for the code vectorization;
- OpenCL and Intel ArBB as a programming solution both for the vectorization and parallelization on CPU;
- OpenCL for GPU programming.
The group participates in the online and offline event reconstruction in:
Research Projects
Cellular Automaton Track Finder
Every track finder must handle a very specific and complicated combinatorial optimization process, grouping together one- or two-dimensional measurements into five-dimensional tracks. The Cellular Automaton (CA) method profits from building up cells, i.e. short track segments with a higher than measurements dimensionality, before starting the combinatorial search. The method is intrinsically local working with data only in a neighborhood. It provides a steady consolidation of the track information identified in the course of the algorithm evolution. In addition, the CA based algorithms can be parallelized in order to be implemented on modern and future many-core CPU/GPU computer architectures.
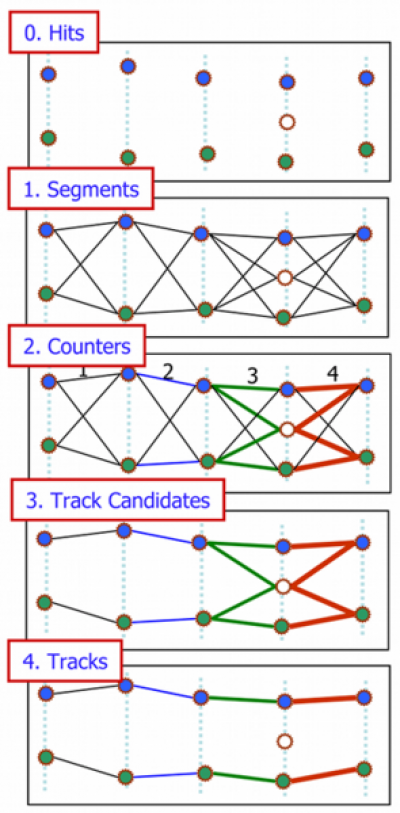
The Cellular Automaton based track finding algorithm can be illustrated py the picture. Here the tracking stations are shown by the vertical dashed lines, hits of two different particles are shown by the blue and green circles, the noise hit is shown by the empty circle. Track segments are shown by the solid lines with their thickness and color corresponding to a possible position of a segment on a track. In the CA method first (1) short track segments, so-called cells, are created. After that the method does not work with the hits any more but instead with the created track segments. It puts neighbor relations between the segments according to the track model here and then (2) one can estimate for each segment its possible position on a track. After this process a set of tree connections of possible track candidates appears. Then one starts with the segments with the largest position counters (3) and follows the continuous connection tree of neighbors to collect the track segments into track candidates. In the last step (4) one sorts the track candidates according to their length and χ2 and then selects among them the best tracks.
Kalman Filter Track Fit
The Kalman filter is widely used for track fitting due to the optimal estimation of the track parameters, locality with respect to the measurements, a suitable track propagation through a non-homogeneous magnetic field and the detector material, simple operation with matrices of small sizes, and the number of computations is proportional to the number of measurements.
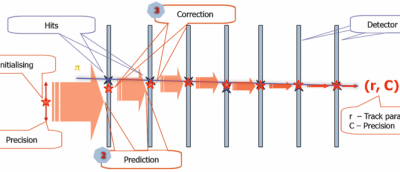
The Kalman filter (1) starts with an arbitrary initial approximation (see picture); (2) adds hits one after the other; (3) refines the state vector and gets the optimal values of the track parameters after the last hit.The Kalman filter is intensively used in the combinatorial part of the CA track finder, therefore its stability in single precision and its fast and optimal implementation on modern CPU and GPU computer systems are crucial.
Starting from the idea of using the SIMD units of modern processors, the KF track fitting algorithm was examined aiming to increase the speed of the event reconstruction. After the detailed optimization of the memory utilization and the numerical analysis, the KF algorithm had been vectorized. To optimize the memory usage the magnetic field approximation is used for particle propagation instead of the magnetic field map, which takes a large fraction of the memory (about 70 MB) and therefore does not fit into the CPU cache memory. The magnetic field is approximated on each detector station plane with the polynomial function of fifth order. During the fit of a track the field behavior between the stations is approximated along the track with a parabola taking field values at the three closest measurements. To stabilize the fit the initial approximation of the track parameters is done by the least square estimator assuming a one-component magnetic field. The first measurement is added in a special way, which also increases the stability of the method: the equations were simplified analytically using a special form of the initial covariance matrix. The track propagation in a non-homogeneous magnetic field is done by an analytic formula, which is based on the Taylor expansion. The formula allows to obtain the same track fit quality as the standard fourth order Runge-Kutta method, while being about 40% faster. Operator overloading has been used to keep flexibility with respect to different CPU/GPU architectures. All these changes have resulted in the increase of the speed of the SIMD KF track fit algorithm down to 1μs per track. This is an improvement by a factor 10000 with respect to the original scalar version of the algorithm.
KF Particle
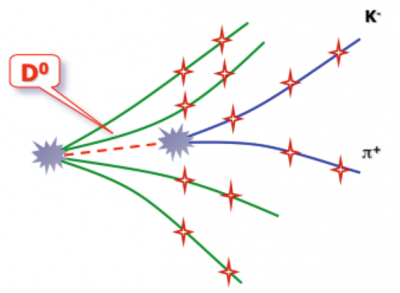
The new physics is now hidden mainly in the properties of very short lived particles, which are not registered in the detectors, but can be reconstructed by its daughter products only. This stage of the event reconstruction is important for the success of the whole experiment. For example an illustration of the D0 decay into K- and π+ is shown: the dashed red line is the D0 trajectory; the green and blue lines show primary and secondary particle trajectories respectively; the red stars are hits in the tracking detectors; the production (primary vertex) and the decay (secondary vertex) points are shown in gray.
The KF Particle software package for the reconstruction of short lived particles has been developed such that all parameters of the particles are provided in the most suitable form for the final physics analysis. The state vector of the parameters contains three coordinates (x, y and z), three components of the momentum (px, py and pz) and the energy (E). These parameters are traditionally used in physics for description of a moving particle, that makes the KF Particle package geometry and experiment independent. KF Particle is based on the Kalman filter method, therefore it provides an estimation of the particle parameters together with their covariance matrix. The package provides also an easy access to such important physical quantities of a particle as mass, decay length, lifetime, momentum, transverse momentum, rapidity, etc. together with their errors. The errors are calculated based on the covariance matrix of the state vector of the particle parameters. The KF Particle package treats all particles (long lived and short lived) in the same way, therefore the reconstruction of decay chains is a simple task within the package.
The fit of a short lived particle is done iteratively. The KF Particle package starts with an initial approximation of the secondary vertex, adds particles one after another, refines the state vector and gives the optimal values after the last particle. If the initial approximation is not known precisely enough the procedure can be repeated several times using the obtained state vector as the initial approximation for the next iteration.
Since the speed of the algorithms is crucial for the modern experiments KF Particle has been fully vectorized and moved into the single precision calculations. To optimize the memory usage by the package the magnetic field approximation is used for the particle propagation instead of the magnetic field map. The magnetic field is approximated by a polynomial function of the second order along the trajectory of the particle and is stored for each particle. Also to speed up the calculations the analytic formula for particle propagation is used.
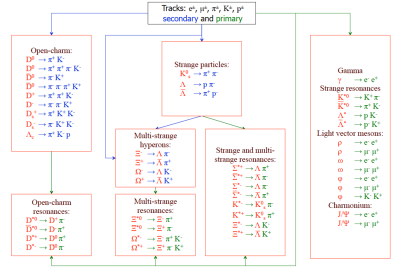
Based on the KF Particle package the KF particle finder has been developed. At the first stage all tracks of the charged particles, which are found by the CA track finder, are divided into two groups: primary and secondary tracks. Strange, multi-strange and open-charm particles are constructed from the secondary tracks taking into account the corresponding mass assumptions for the tracks. Combining the obtained strange and open-charm particles with the primary tracks, strange, multi-strange and open-charm resonances are constructed. The primary tracks with the corresponding mass hypothesis are combined into strange resonances (which decay into charged long lived particles), light vector mesons and charmonium. The search of in total about 50 decay modes of short lived particles is implemented in the KF particle finder. Taking into account the topology of the decay and χ2 criteria the particle candidates are then selected and stored.
Research of Ivan Kisel
Overview
The track and particle reconstruction is a task, which needs a lot of computational power. At the same time all modern high energy physics experiments operate with huge data rates and require fast reconstruction procedures. In order to operate effectively in such difficult conditions the full utilization of the computer power is required. Parallel programing is considered now as the only way to utilize the full power of CPU and GPU, since all modern CPUs and GPUs have more than one core. They are also equipped with SIMD units. Therefore the developed algorithms are implemented using:
- headers overloading SIMD instructions and a Vc library for the code vectorization;
- OpenCL and Intel ArBB as a programming solution both for the vectorization and parallelization on CPU;
- OpenCL for GPU programming.
The group participates in the online and offline event reconstruction in:

Research Projects
Cellular Automaton Track Finder
Every track finder must handle a very specific and complicated combinatorial optimization process, grouping together one- or two-dimensional measurements into five-dimensional tracks. The Cellular Automaton (CA) method profits from building up cells, i.e. short track segments with a higher than measurements dimensionality, before starting the combinatorial search. The method is intrinsically local working with data only in a neighborhood. It provides a steady consolidation of the track information identified in the course of the algorithm evolution. In addition, the CA based algorithms can be parallelized in order to be implemented on modern and future many-core CPU/GPU computer architectures.
The Cellular Automaton based track finding algorithm can be illustrated py the picture. Here the tracking stations are shown by the vertical dashed lines, hits of two different particles are shown by the blue and green circles, the noise hit is shown by the empty circle. Track segments are shown by the solid lines with their thickness and color corresponding to a possible position of a segment on a track. In the CA method first (1) short track segments, so-called cells, are created. After that the method does not work with the hits any more but instead with the created track segments. It puts neighbor relations between the segments according to the track model here and then (2) one can estimate for each segment its possible position on a track. After this process a set of tree connections of possible track candidates appears. Then one starts with the segments with the largest position counters (3) and follows the continuous connection tree of neighbors to collect the track segments into track candidates. In the last step (4) one sorts the track candidates according to their length and χ2 and then selects among them the best tracks.

Kalman Filter Track Fit
The Kalman filter is widely used for track fitting due to the optimal estimation of the track parameters, locality with respect to the measurements, a suitable track propagation through a non-homogeneous magnetic field and the detector material, simple operation with matrices of small sizes, and the number of computations is proportional to the number of measurements.

The Kalman filter (1) starts with an arbitrary initial approximation (see picture); (2) adds hits one after the other; (3) refines the state vector and gets the optimal values of the track parameters after the last hit.The Kalman filter is intensively used in the combinatorial part of the CA track finder, therefore its stability in single precision and its fast and optimal implementation on modern CPU and GPU computer systems are crucial.
Starting from the idea of using the SIMD units of modern processors, the KF track fitting algorithm was examined aiming to increase the speed of the event reconstruction. After the detailed optimization of the memory utilization and the numerical analysis, the KF algorithm had been vectorized. To optimize the memory usage the magnetic field approximation is used for particle propagation instead of the magnetic field map, which takes a large fraction of the memory (about 70 MB) and therefore does not fit into the CPU cache memory. The magnetic field is approximated on each detector station plane with the polynomial function of fifth order. During the fit of a track the field behavior between the stations is approximated along the track with a parabola taking field values at the three closest measurements. To stabilize the fit the initial approximation of the track parameters is done by the least square estimator assuming a one-component magnetic field. The first measurement is added in a special way, which also increases the stability of the method: the equations were simplified analytically using a special form of the initial covariance matrix. The track propagation in a non-homogeneous magnetic field is done by an analytic formula, which is based on the Taylor expansion. The formula allows to obtain the same track fit quality as the standard fourth order Runge-Kutta method, while being about 40% faster. Operator overloading has been used to keep flexibility with respect to different CPU/GPU architectures. All these changes have resulted in the increase of the speed of the SIMD KF track fit algorithm down to 1μs per track. This is an improvement by a factor 10000 with respect to the original scalar version of the algorithm.
KF Particle
The new physics is now hidden mainly in the properties of very short lived particles, which are not registered in the detectors, but can be reconstructed by its daughter products only. This stage of the event reconstruction is important for the success of the whole experiment. For example an illustration of the D0 decay into K- and π+ is shown: the dashed red line is the D0 trajectory; the green and blue lines show primary and secondary particle trajectories respectively; the red stars are hits in the tracking detectors; the production (primary vertex) and the decay (secondary vertex) points are shown in gray.

The KF Particle software package for the reconstruction of short lived particles has been developed such that all parameters of the particles are provided in the most suitable form for the final physics analysis. The state vector of the parameters contains three coordinates (x, y and z), three components of the momentum (px, py and pz) and the energy (E). These parameters are traditionally used in physics for description of a moving particle, that makes the KF Particle package geometry and experiment independent. KF Particle is based on the Kalman filter method, therefore it provides an estimation of the particle parameters together with their covariance matrix. The package provides also an easy access to such important physical quantities of a particle as mass, decay length, lifetime, momentum, transverse momentum, rapidity, etc. together with their errors. The errors are calculated based on the covariance matrix of the state vector of the particle parameters. The KF Particle package treats all particles (long lived and short lived) in the same way, therefore the reconstruction of decay chains is a simple task within the package.
The fit of a short lived particle is done iteratively. The KF Particle package starts with an initial approximation of the secondary vertex, adds particles one after another, refines the state vector and gives the optimal values after the last particle. If the initial approximation is not known precisely enough the procedure can be repeated several times using the obtained state vector as the initial approximation for the next iteration.

Since the speed of the algorithms is crucial for the modern experiments KF Particle has been fully vectorized and moved into the single precision calculations. To optimize the memory usage by the package the magnetic field approximation is used for the particle propagation instead of the magnetic field map. The magnetic field is approximated by a polynomial function of the second order along the trajectory of the particle and is stored for each particle. Also to speed up the calculations the analytic formula for particle propagation is used.
Based on the KF Particle package the KF particle finder has been developed. At the first stage all tracks of the charged particles, which are found by the CA track finder, are divided into two groups: primary and secondary tracks. Strange, multi-strange and open-charm particles are constructed from the secondary tracks taking into account the corresponding mass assumptions for the tracks. Combining the obtained strange and open-charm particles with the primary tracks, strange, multi-strange and open-charm resonances are constructed. The primary tracks with the corresponding mass hypothesis are combined into strange resonances (which decay into charged long lived particles), light vector mesons and charmonium. The search of in total about 50 decay modes of short lived particles is implemented in the KF particle finder. Taking into account the topology of the decay and χ2 criteria the particle candidates are then selected and stored.