In 2017 we devoted a new method using deep learning technique to construct an equation-of-state(EoS) meter to better understand QCD matter created from heavy-ion collisions. We showed that complex hydro evolution which is mimicking the heavy-ion collisions, even though there are many different physical factors and parameters involved would kinkily influence the final emitted partial spectra and thus hinder a conventional analysis of pinning down the phase structure or transition information during the collision, the deep convolutional neural network (CNN) is capable of disentangling the hidden correlations and find direct efficient mapping from the output particle spectra to phase transition information embedded in the evolution. This thus provides us an useful tool to unveil hidden knowledge from the highly implicit evolutions/dynamics. The work has been published in Nature Communications in 2018: https://www.nature.com/articles/s41467-017-02726-3

We further pushed this project from three different aspects into more realistic situations: 

1. We included the afterburner hadronic cascade which is essential but missed in the previous study by employing a hybrid simulation consisting of a 2+1D hydrodynamic and UrQMD as after-burner (together with Dr. Yilun Du). The results was published in Eur.Phys.J. C80 (2020) no.6, 516. 
2. We considered phase non-equilibrium possibility during its transition by allowing spinodal decomposition phenomenon in heavy-ion collisions (together with Dr. Jan Steinheimer). The work now is published in JHEP 1912 (2019) 122. 
3. We considered the experimental detector simulation effects into model simulation, to which only final tracks and hits are recordes and taken to be input of the deep learning algorithms (together with Manjunath Omana Kuttan and Jan Steinheimer). We published our first step work in Phys.Lett. B811 (2020) 135872.

We explored the perspectives of Deep Learning in the context of lattice quantum field theory. We take for first step deep learning in the two-dimensional complex scalar field at nonzero temperature and chemical potential with a nontrivial phase diagram. A neural network is successfully trained to recognize the different phases of this system and to predict the value of various thermodynamic observables based on the microscopic configurations. We analyze a broad range of chemical potentials and find that network is robust and able to recognize patterns far away from the point where it was trained. We found that the network is capable of recognizing correlations in the system between various observables and phase classification without the specific guidance. Very interestingly it discovered a correlation beyond the conventional analysis which enabled it to use even restricted input to recognize phase transition. The regression network also showed remarkable performance on physical observables (number density n and squared field) prediction when tested at chemical potential beyond the training set. This provide an effective high-dimensional non-linear regression method with limited data points. 

Aside from these discriminative tasks, which belongs to supervised learning, we further proposed an unsupervised generative network GAN to produce new quantum field distribution. An implicit local constraint (closed-loop) fulfilled by the physical configurations was found to be automatically captured by our generative model GAN. We found that the generator in GAN can represent well the distribution of prominent observables. By adding conditional information about parameters, we also demonstrated that the GAN can disentangle the dependency of system's underlying distribution on the physical paramter and can generalize beyond the training set parameter space for configuration generation. This provides an more efficient scenario generation way which bypass the conventional Markov-Chain Monte Carlo process, and thus being faster and memory light.

The paper is published as Rapid Communications in Phys.Rev. D100 (2019) no.1, 011501.

We propose a Multi-channel Autoregressive Networks for variational calculation of continuous spin system, in which the Kosterlitz-Thouless phase transition was recognized. Meanwhile the Vortices as the quasi-Long Range Order(LRO) are accurately detected by the ordering neural networks on a periodic square lattice. By learning the microscopic possibility distributions from macroscopic thermal distribution, the free energy is directly calculated and vortices(anti-vortices) pair emerge with temperature rising. As a more precise estimation, the helicity modulus is evaluated to anchor the transition temperature. Although time-consuming of the training process is inevitably increasing with the lattice size, the training time remains unchanged around the transition temperature, at which the critical slowing down (CSD) problem is partially avoided. This work is now online arXiv:2005.04857.

We further proposed a general framework based on the autoregressive network to extract microscopic interactions from raw configurations. The approach replaces the modeling Hamiltonian by the deep autoregressive neural networks, in which the interaction is encoded efficiently. It can be trained with data collected from Ab-initio computations or experimental measurement. The well-trained neural networks give an accurate estimation of the possibility distribution of the configurations at fixed external parameters. It can be spontaneously extrapolated to detect the phase structures since classical statistical mechanics as prior knowledge here. We apply the approach to a 2D spin system, training at a fixed temperature, and reproducing the phase structure. Scaling the configuration on lattice exhibits the interaction changes with the degree of freedom, which can be naturally applied to the experimental measurements. Our approach bridges the gap between the real configurations and the microscopic dynamics with an autoregressive neural network. The work is now online arXiv:2007.01037.

As further development goal, we target at reconstructing dynamics of non-equilibrium many-body systems by developing network that can simulate the evolution of the physical system in a suitable latent space representation. 

Computational Fluid Dynamics (CFD) nowadays have broad applications in both scientific and industrial researches, like in Heavy-ion collisions, Neutron Star merger with Gravitational wave emission simulations, Engineering design optimization for automobile or aerial vehicle, etc. The fluid dynamics simulation is in general expensive/time-consuming and in some cases (turbulence/cavitation flow) can not cover the full complex phenomena/interactions realistically. Priviously in the context of heavy-ion collisions simulated with relativistic hydrodynamics, we put forward a deep learning approach to learn the early-time medium's properties from the accessible final output experimentally, we showed that DL can help us constructing equation-of-state meter based on the final spectrum from the flowing system regardless other physics uncertainties which traditionally hinder strongly the mapping's decoding. This implies the ability of DL to caputre the dynamics for flowing system. In this project we systematically explore the usage of Deep Learning tools to improve/speed-up the CFD simulation on GPUs. We first develop DL algorithms for Riemann Solvers which is essential part in fluid simulation, both RNN and GAN would be explored here starting with simple waves, further test on converging flow and shock tube cases. Further we develop the DL-based simulation tool for normal non-relativistic hydrodynamics which can learn the map/evolution to final shot of fluid evolution automatically, conditioned on diverse initial profiles with different medium properties. As a final goal we will generalize the development to including turbulence/cavitation and relativistic case, and apply it for both fundamental scientific and industrial CFD analysis/emulation. The relativistic one will be applied for gravitational wave emission from neutron star mergers to help understand neutron star inner properties. The turbulence one will be applied to optimize valve geometry design to meet custom-defined functionality without expensive trial-and-error iteration. This will take 6 to 9 months. To get reasonable resolution in simulation the space-time grids shouldn't be small which acquires multi-GPUs in the calculation. 

Besides physics study, we deploy deep learning application in industrial, like our collaboration with Samson AG in frankfurt. Samson AG is renown in valve manufacturing. Under the same spirit in pursuing the Industrial 4.0 academically, we conducted ‘Smart Valve’ project which aims at giving normal valve the ability to talk to outside and communicate with each other. In the first step, with close collaboration with the new innovation center at Samson AG, the acoustic signal is recorded with different physical processing parameters and valve states, then we use deep learning to construct a ‘brain’ for the valve based on the sound signals to tell if there’s leakage for the valve, to estimate the flow rate being inside and also the pressure ratio, to detect cavitation/turbulent flow state for the running valve. These information like the cavitation detection is critical for security and lifecycle maintance for the system. The technique thus would save a lot of manpower and help doing anomaly detection and safety insuring for valve/pipe system like underground or large-scale industrial devise. The technique is also applied in seismology for earthquake magnitude prediction.

For heavy-ion-collisions, as was shown in model simulations, deep learning can help decoding important underlying physical properties from the final accessible particle distribution. This leads to the idea of directly applying deep learning in collision experiments for both data analysis and detector design. Based on our previous works we got a BMBF funding to support this project since 2019. 

We plan to study the influence of event reconstruction from realistic experimental side on physics extraction using deep learning study. The acceptance limitation, possible track-fit and finder uncertainties will be taken into account by detector simulation and corresponding methods. The trained algorithm will be tested on real experimental data. Further more, we develp AI algorithm to control the quality of the signal and to reduce the noise from aged detector sub-systems as part of the calibration.

As a first step study we included the detector simulation (with acceptance/efficiency corrections considered) for CBM experiments into the DL-analysis tool development, we constructed online impact parameter 'b-meter'  with a pointnet which can directly analyze the raw track records on event-by-event basis from the detectors and shows good performance/resolution, which outperform the conventional Glauber model analysis and bypassed 'manipulation' on raw uncorrected data from experiments or event ensemble collection, This can be easily extended to other physics real time analysis and help realizing event selection as well. This work is published in Phys.Lett. B811 (2020) 135872.

We develop machine learning based gravitational wave analyser for neutron star–neutron star collapse for extracting information like tidal deformabilities, mass and and so to constrain the EoS of matter in NS interior. It has been shown in litrature that ML techniques are reliable for the classification of time-series waveforms from binary black hole (BBH) and BNS coalescences. We tested if the same classification techniques are suitable to differentiate EoSs that describe matter in NSs. In order to do this, gravitational waveform templates for different binary NS masses has to be generated which take into account the EoS. However, generating model waveforms for coalescing binary neutron stars is a challenging problem. Numerical relativity simulations are computationally expensive, whereas the limits are reached for the post Newtonian (PN)

methods. We took waveform models from the LALSuite library. Model waveforms like the PhenomDNRT, PhenomPNRT, SEOBNRT, etc, which use the aligned-spin point-particle model (with and without precession effects), and the aligned-spin point-particle effective-one-body (EOB) model, perform up to a high level of accuracy when tested with NR simulations. All these waveforms are generated by adding tidal effects to their corresponding BBH baseline waveforms.

The classification of GW signals in frequency-domain from BBH, BNS mergers and noise, generated using LaLSuite, is already in progress using Deep Learning (DL, a branch of ML) techniques. This will further be extended to classify the NS EoSs by generating waveforms that are indirectly dependent on the EoS. Though these waveforms do not explicitly involve the thermodynamic properties that define the EoS, they depend on tidal properties which are unique for each EoS. This can provide evidence that ML can help decode NS matter properties from the GW emission of BNS mergers. As a preliminary problem, GW signals generated from two EoSs namely, DD2 and BHBΛφ will be tested for classification. The BHBΛφ EoS, is generated by including hyperonic matter in the already existing DD2 model. It is the only EoS with hyperons satisfying the 2M limit, and is used for BNS merger simulations widely. Apart from the EoS classification, this solution can also explain the imprint of hyperonic matter in GWs.

While the waveforms in the LALSuite library are widely used in LIGO analysis of GW data, their accuracy has not yet been confirmed. Therefore, this study will be further followed up with waveforms from the Computational Relativity (CoRe) Database. CoRe is a public database which contains gravitational waveform models from BNS mergers obtained with numerical simulations, that are consistent with general relativity. The numerical methods used here implement the (3+1) dimensional general relativistic hydrodynamics of a coalescing BNS system. The algorithm will be improvised accordingly if required. Once the data from the O3 run of the GW detectors is released, each of the waveforms will be analyzed in order to constrain or determine the EoS using the ML/DL algorithm.

Time and again, catastrophic earthquakes have disastrously impacted civilization, devastated urbanization, annihilated human lives and created substantial setbacks in the socio-economic development of a region. Earthquakes are considered a major menace among all the natural hazards, affecting more than 80 countries and causing over 1.6 million deaths each year. The impact due to an earthquake, interacting with a vulnerable social system continues to grow due to phenomenal rise in the global population and growth of mega cities and their exposure in the earthquake prone regions across the globe. A single earthquake may take up to several hundred thousand lives (e.g., the 2010 Haiti earthquake which took 222570 human lives) and cause huge economic loss (e.g., the 2011 Tohoku earthquake caused the direct damage worth US $211 billion). A large earthquake can trigger an ecological disaster if it occurs in close vicinity to a dam or a nuclear power plant (e.g. the Tohoku earthquake and subsequent tsunami damaged the Fukushima Dai-ichi nuclear power plant). Approximately a million earthquakes with magnitude greater than two are reported each year among which nearly a thousand are strong enough to be felt and about a hundred events destruction depending on physical vulnerability and exposure.

Earthquakes are inevitable and considered extremely difficult to predict. The analysis of past seismic stress history of an active fault can help in understanding the stress build-up and local breaking point of the fault. However, analysing and interpreting the abundant seismological dataset is a time consuming task. The implementation of Artificial Intelligence (AI) powered by deep learning algorithm has the potential to decipher the complex patterns in past stress history that is nearly impossible for conventional methods. This careful implementation of deep learning algorithm will significantly improve the early warning system and thus could help save human lives.

Our group is currently attempting to understand the intricate pattern associated with the seismic stress released by various Deep Learning/Machine Learning algorithm in the past earthquake data available for the South-East Asian country which lies on the Pacific Ring of Fire, Indonesia. The spatial and magnitude distribution of the earthquakes is shown above, while the frequency of earthquakes is shown in the figure below. Owing to the high frequency of earthquakes striking every year from different epicentres, the region provides a huge database which has been assembled during the first part of the project. This newly composed dataset is now being used to train a machine/deep learning algorithm to decipher time and spatial correlations in the stress accumulation and release pattern, consequently leading to earthquakes. We are considering both small and large magnitude earthquakes to generate a localised time series to understand the seismic history of the region. Training a machine learning algorithm by using the earthquake dataset of past 50 years allows us to study possible predictions on the stress release for the coming year/month/week.

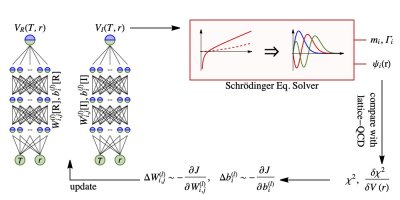
One recent research focus of my group is AI for inverse problems (IP). IPs occur in many research areas, especially in the context of ErUM related fundamental physics, also in other scientific and engineering areas. We devised a methodology for IPs which integrates our physics-priors knowledge into the specific IPs solving process with deep learning representation together with gradient-based optimization (i.e. automatic differentiation – AD framework) to perform Bayesian inference on the problem. We demonstrated the developed methodology in several IPs raised in high energy nuclear physics (can also be easily generalized to other physics areas as well). (1) We first deploy the above AD-based approach to reconstruct spectral functions from Euclidean correlation functions which has been proven ill-posed especially with limited and noisy measurements. In our method the spectral is represented by DNNs while the reconstruction turns out to be optimization within AD under natural regularization to fit the measured correlators. We demonstrated and proved that the network with weight regularization can provide non-local regulator for this IP. Compared to conventional maximum-entropy-method (MEM), our method achieved better performance in realistic large-noise situation. It’s for the first time to introduce non-local regulator using DNNs for the problem and is an inherent advantage for the method, which can promisingly lead to substantial improvements in related problems and IPs. (2) We applied the method to reconstruct the fundamental QCD force – heavy-quark potential – from lQCD calculated bottomonium in-medium spectrum. Both the radius and temperature dependence of the interaction are well reconstructed via inverse the Schroedinger equation given limited and discretized bottomonium low-lying states mass and width. (3) We also demonstrated the method’s ability to infer neutron star EoS from astrophysical observables, with exciting results on closure tests for reasonable EoS reconstruction based on finite noisy M-R observables. Compared to conventional approaches our method holds unbiased representation for the EoS and bare interpretable Bayesian picture for the reconstruction.

References:

1. Rethinking the ill-posedness of the spectral function reconstruction – why is it fundamentally hard and how Artificial Neural Networks can help, By: L. Wang, S. Shi, K. Zhou*. arXiv:2201.02564

2. Neural network reconstruction of the dense matter equation of state from neutron star observables, By: S. Soma, L. Wang, S. Shi, H. Stoecker, K. Zhou*.  arXiv:2201.01756

3. Automatic differentiation approach for reconstructing spectral functions with neural networks, By: L. Wang, S. Shi, K. Zhou*.  arXiv:2112.06206

4. Reconstructing spectral functions via automatic differentiation, By: L. Wang, S. Shi, K. Zhou*.  arXiv:2111.14760

5. Heavy Quark potential in QGP: DNN meets LQCD, By: S. Shi, K. Zhou*, J. Zhao, S. Mukherjee, P. Zhuang.  Physical Review D 105 (2022)1,014017,  arXiv:2105.07862